1. Variance-inflation factors

모델 > 수치적 진단 > 분산-팽창 요인

Models > Numerical diagnostics > Variance-inflation factors

Linux 사례 (MX 21)

선형모델에서 유의미한 설명변수들을 찾고 선택하는 것과 관련된 여러 기법이 있다. 아울러 설명변수들 사이의 관계, 서로에 대한 영향력의 크기에 대한 문제의식도 있다. 예를 들어, 데이터셋에 있는 여러개의 변수들 중에서 세개의 변수를 설명변수라고 선택을 했는데, 하나의 설명변수가 나머지에 큰 영향을 미치거나 또는 다른말로 변수들끼리의 연동성의 커서 독립된 설명변수들로 보기 어려운 경우가 발생할 수도 있다. 이 때 설명변수들의 독립성에 관한 점검 기법으로 '분산-팽창 요인(variance-inflation factor)'이 사용된다.

require(car)
?vif           # vif 함수는 car 패키지에 포함되어 있다.

carData 패키지에 있는 Duncan 데이터셋으로 연습해보자.

https://rcmdr.tistory.com/189

Duncan 데이터셋

아래와 같은 스크립트의 흐름이다.

data(Duncan, package="carData")
summary(Duncan)

LinearModel.1 <- lm(prestige ~ education + income, data=Duncan)
summary(LinearModel.1)
LinearModel.2 <- lm(prestige ~ education + income + type, data=Duncan)
summary(LinearModel.2)
vif(LinearModel.1)    # LinearModel.1의 분산팽창요인
round(cov2cor(vcov(LinearModel.1)), 3) # Correlations of parameter estimates
vif(LinearModel.2)    # LinearModel.2의 분산팽창요인
round(cov2cor(vcov(LinearModel.2)), 3) # Correlations of parameter estimates

'통계 > 적합성 모델 > 선형 모델...' 기능을 통하여 LinearModel.1과 LinearModel.2를 만든다.

Linux 사례 (MX 21)

Linux 사례 (MX 21)

LinearModel.1과 LinearModel.2의 분산-팽창 요인(Variance-inflation factors)을 차례로 계산한다.

Linux 사례 (Mx 21)

Linux 사례 (MX 21)

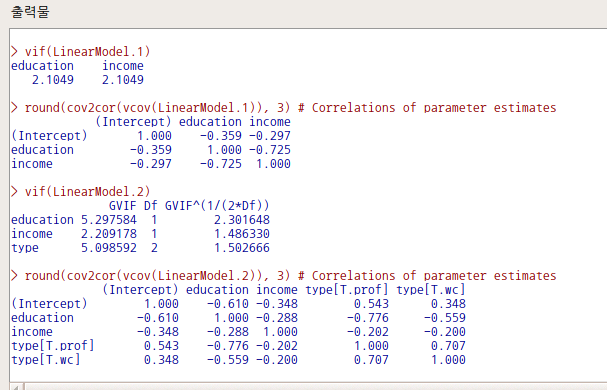
LinearModel.1과 LinearModel.2의 vif() 결과는 아래와 같다. LinearModel.1과 LinearModel.2의 vif() 결과가 다른 형식을 취한 이유는 LinearModel.2에 type이라는 요인형 변수가 있기 때문이다.

Linux 사례 (MX 21)